Supports are arguably one of the most important aspects of a structure, as it specifies how the forc…
Read MoreEngineering stress-Strain and True stress-strain
Engineering stress-Strain and True stress-strain
In engineering and materials science, stress–strain curve for a material gives the relationship between stress and strain. That is obtained by gradually applying load to a test coupon and measuring the deformation from tensile testing, in which the stress and strain can be determined. These curves reveal many properties of materials, such as Young’s modulus, the yield strength, the ultimate tensile strength and so on.
Different materials exhibit different behaviours/trends under the same loading condition.
More traditional engineering materials such as concrete under tension, glass metals, and alloys exhibit adequately linear stress-strain relations until the onset of yield point.
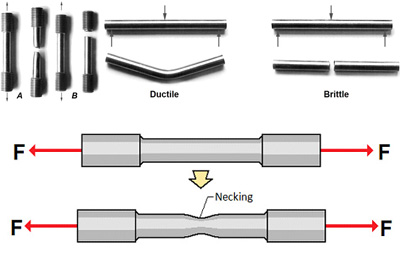
Axial tensile test and bending test for two different materials:
A is a ductile material, and B is a brittle material.
Actual stress & strain (w.r.t to change in dimensions) are used for accurate definition of plastic behaviour of ductile materials by considering the actual dimensions.
Brittle materials usually fracture(fail) shortly after yielding or even at yield points whereas alloys and many steels can extensively deform plastically before failure. The characteristics of each material should be chosen based on the application and design requirements.
The ductile material rod has been experimented with in the given way. Think about pulling a bar in tension. Load divided by cross-sectional area is force or stress. But what cross-section are you considering? Before starting that pull, the bar had a known cross-section of, let’s say, 0.5″ wide x metal thickness. It’s easy to measure these since it is your starting material. At any load, the engineering stress is the load divided by this initial cross-sectional area. While you are pulling, the length increases, but the width and thickness shrink. At any load, the true stress is the load divided by the cross-sectional area at that instant. Unless thickness and width are being monitored continuously during the test, you cannot calculate true stress. It is, however, a much better representation of how the material behaves as it is being deformed, which explains its use in forming simulations. In circle grid analysis, engineering strain is the percent expansion of the circle compared to the initial diameter of the circle.
This shows the cross-section of the specimen has changed during the experiment process.
The cross-section does not remain constantly and will be different from the given value of diameter. This stress is called True Stress. The applied force is divided by the area of the section at that instant.
Before going to the actual definition of engineering stress/strain and true stress/strain, we will focus on a material curve. It is observed that the most obvious thing you may notice is that the true stress-strain curve never decreases. That is because the material never gets weaker! The decrease in the engineering stress is an illusion created because the engineering stress doesn’t consider the decreasing cross-sectional area of the sample.
The strain is set to the horizontal axis and stress is set to the vertical axis. The stress-strain curve for material is plotted by elongating the sample and recording the stress variation with strain until the sample fractures. It is often assumed that the cross-section area of the material does not change during the whole deformation process. This is not true since the actual area will decrease while deforming due to elastic and plastic deformation as discussed earlier. The curve based on the original cross-section and gauge length is called the engineering stress-strain curve, while the curve based on the instantaneous cross-section area and length is called the true stress-strain curve.
True stress and strain are different from engineering stress and strain.
In a tensile test, true stress is larger than engineering stress and true strain is less than engineering strain. The difference between the true and engineering stresses and strains will increase with plastic deformation. At low strains (in elastic region), the differences between the two are negligible.
True stress is the applied load divided by the actual cross-sectional area (the changing area with time) of material. Engineering stress is the applied load divided by the original cross-sectional area of a material. Also known as nominal stress.
DEFINITION &EQUATION:
Engineering stress is the applied load divided by the original cross-sectional area of a material. Also known as nominal stress.
True stress is the applied load divided by the actual cross-sectional area (the changing area with respect to time) of the specimen at that load
Engineering strain is the amount that a material deforms per unit length in a tensile test. Also known as nominal strain.
True strain equals the natural log of the quotient of current length over the original length.
|
|
Load |
|
|
Initial Cross-Sectional area of the specimen |
|
|
The cross-Sectional area of specimen at a given instance of time |
|
|
The original value of the length of the specimen |
|
|
Length of specimen at given instance of time |
Relation between engineering stress and true stress :
Assuming that there is no volume change during deformation The analytical equation for converting engineering stress-strain to true stress-strain are given below:
To conclude
-
As yield & failure are nearer in brittle material, the variation between engineering stress/strain and true stress/strain is negligible
-
Ductile material till elastic limit or yielding point considered to the same values in both the engineering & true stress-strain properties
-
The variation is considerably high in the plastic zone of ductile materials after ultimate load application.
Learn More About Engineering stress-Strain and True stress-strain at the Best CAD & CAE Institute in India - artem.co.in

4 years ago / 0
Petrol Vs Diesel Engine Engines are the powerhouse of vehicles and systems. It provides the energ…
Read More
© Copyright 2021 Artem Academy. All rights reserved.
Designed & Developed by Colour Moon